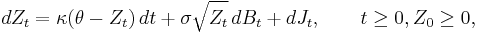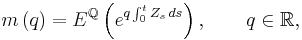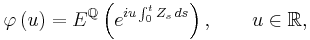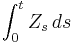Basic affine jump diffusion

In probability theory, a basic affine jump diffusion (basic AJD) is a stochastic process Z of the form

dZ_t=\kappa (\theta -Z_t)\,dt%2B\sigma \sqrt{Z_t}\,dB_t%2BdJ_t,\qquad t\geq 0, Z_{0}\geq 0,

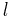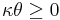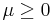where B is a standard Brownian motion, and J is an independent compound Poisson process with constant jump intensity l and independent exponentially distributed jumps with mean \mu . For the process to be well defined, it is necessary that \kappa \theta \geq 0 and \mu \geq 0 . A basic AJD is a special case of an affine process and of a jump diffusion. On the other hand, the Cox–Ingersoll–Ross (CIR) process is a special case of a basic AJD.

Basic AJDs are attractive for modeling default times in credit risk applications,[1][2][3][4] since both the moment generating function

m\left( q\right) =E^{\mathbb{Q}}\left( e^{q\int_0^t Z_s \, ds}\right) ,\qquad q\in \mathbb{R},

and the characteristic function

\varphi \left( u\right) =E^{\mathbb{Q}} \left( e^{iu\int_0^t Z_s \, ds}\right) ,\qquad u\in \mathbb{R},

are known in closed form.[3]

The characteristic function allows one to calculate the density of an integrated basic AJD

\int_0^t Z_s \, ds

by Fourier inversion, which can be done efficiently using the FFT.

References

  1. ^ Darrell Duffie, Nicolae Gârleanu (2001). "Risk and Valuation of Collateralized Debt Obligations". Financial Analysts Journal 57: 41–59.  Preprint
  2. ^ Allan Mortensen (2006). "Semi-Analytical Valuation of Basket Credit Derivatives in Intensity-Based Models". Journal of Derivatives 13: 8–26.  Preprint
  3. ^ a b Andreas Ecker (2009). "Computational Techniques for basic Affine Models of Portfolio Credit Risk". Journal of Computational Finance 13: 63–97.  Preprint
  4. ^ Peter Feldhütter, Mads Stenbo Nielsen (2010). Systematic and idiosyncratic default risk in synthetic credit markets.  Preprint